Objective Function and Regularization etc (ML)
Regression
While learning ML algorithms, one often comes across new concepts and
terms .In this post, I try to cover some notes on optimization, cost function,
regularization w.r.t regression. The notes are collated for easy access and
reference from the rich content made available by experts.
To fit a model, it often boils down to finding an equation that passes
through all (most) of the training data points. Say if it’s a linear plane, one
tries to find a line that goes through all the points.
Once an initial line is drawn, we use different distance measures to
find it it’s the best line or not.
Say the line is given by equation below
The problem boils
down to how to find the value of  such
that for values of x, predicted values of y is closer to actual value of y .
such
that for values of x, predicted values of y is closer to actual value of y .
In regression, OLS is a widely used cost function,
where we try to find the line such that sum of square of distances of points and the line
is minimum.
Optimization and Cost Function
Cost function can be defined as

Optimization here refers to optimize the parameter values so that cost
function is minimum.
You will hear the word optimization often when you deal with modelling. Optimization
is generally defined as maximizing or minimizing some function. The function
helps to determine which solution is the best. In this context, the function is
called cost function, or objective function, or energy. Common context of usage
are minimal cost, maximal profit, minimal error, optimal design.
Optimization is a field in itself. I will just try to post a brief from
various web pages. Different libraries provide specific optimization/algorithms.
Awareness of which one is suited for which type of problems is desirable. Some
of the different optimization techniques/optimizers that you may hear are
Gradient descent
Stochastic gradient descent (SGD)
Conjugate Gradient Descent
Newton Methods
BFGS
Limited-memory BFGS (L-BFGS)
To calculate the  and
and  ,
we can use Gradient Descent or Normalization techniques.
,
we can use Gradient Descent or Normalization techniques.
Another important concept in these
algorithms is Regularization. If we see
Is not fitting well, we consider adding more terms like below and try to
fit..
Adding
more terms may actually over fit the training data well…ie a line that passes
through all points of training, but when used to predict, it doesn’t do well.
To
handle over fitting, there are few approaches like reduce number of features by
finding which feature contributes better to model and Regularization. One of
the merits of reducing features or reducing dimension is you work with less and
what’s significant with ease…A drawback though is there may be some
contributions of those features you discarded as not so significant and this
may impact a bit of accuracy.
Regularization is a common technique to avoid over fitting and still keeping all the features. How it
works it though it keeps  it reduces/optimizes value of
it reduces/optimizes value of  .
Make
.
Make  very small so that Xi
very small so that Xi contribution is there but small.
contribution is there but small.
Regularization
works well and is preferred in cases where you have lot of features and each of
the features contribute a bit in predicting y.
Now
we have something referred to as Objective function.
The objective function ff has two parts: the regularizer that controls
the complexity of the model, and the loss/cost that measures the error of the
model on the training data. The loss/cost function is typically a convex function.
The fixed regularization parameter λ defines the trade-off between the two
goals of minimizing the loss (i.e., training error) and minimizing model
complexity (i.e., to avoid over fitting).
There are 3 common forms of regularization used and associated
regression names associated.
L1 Regularization, also known as Lasso Regression uses regularization
term that is the first norm.
Ie. adds penalty equivalent to absolute value of the magnitude of
coefficients.
•
Limitations:
•
If , the LASSO
selects at most variables. The number of selected variables is
bounded by the number of observations.
•
The LASSO fails to do grouped
selection. It tends to select one variable from a group and ignore the
others.
L2 Regularization also known as Ridge Regression uses L2 by adding
penalty equivalent to square of the magnitude of coefficients
•
The tuning parameter serves to control the relative impact of these two
terms on the regression coefficient estimates.
•
Selecting a good value for  is critical; cross-validation is used for
this.
is critical; cross-validation is used for
this.
Elastic Net…that’s a combination of L1/L2.
•
Elastic Net penalize the size of the regression coefficients based on both
their norm and their norm :


•
The norm penalty generates a sparse model.
•
The norm penalty:
•
Removes the limitation on the
number of selected variables.
•
Encourages grouping effect.
•
Stabilizes the regularization path.
Many machine learning methods can be formulated as a convex optimization
problem i.e finding a minimizer for function.
Under the hood, linear methods use
convex optimization methods to optimize the objective functions. Currently, most algorithm APIs support Stochastic
Gradient Descent (SGD), and a few support L-BFGS. Spark MLib uses two methods, SGD and L-BFGS.

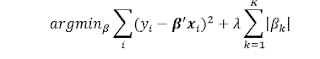


Comments
Post a Comment