Statistics Learning for Data Science-2 of N (Static Scores - Z Score)
Standard Score:
Z-Score
Helps to compare apples and oranges..i.e two different data sets.
Basically it helps to standardize and is known as a standard score statistics.
It comes handy is scenarios like you want to compare tow different team's performance..say Team A playing in Tournament X with Team B playing in Tournament Y..or
say how well your son performed in English vs Maths in his class.
Z score for a value is defined as =(X-Mean)/Std.Dev
i.e how far is the the value from mean in terms of Std Dev.
http://web.cortland.edu/andersmd/STATS/stdscore.html
A z Scoreis an actual or raw score converted intostandard deviation (SD) units -- hence the term standard score -- sothat it can be placed on the normal distribution curve. A z score indicates how much ascore deviates from the mean of the distribution. Simply knowing a z scoreoffers no information about the raw score, but it indicates how well a persondid compared to other test-takers in the norm group.
The units of a z score are from -3 SD to +3 SD, and 0 equals the mean.Therefore, positive z scores exceed the mean, while negative z scores are lessthan the mean.
There are few good examples illustrated at site
https://statistics.laerd.com/statistical-guides/standard-score-2.php
Z-Score
Helps to compare apples and oranges..i.e two different data sets.
Basically it helps to standardize and is known as a standard score statistics.
It comes handy is scenarios like you want to compare tow different team's performance..say Team A playing in Tournament X with Team B playing in Tournament Y..or
say how well your son performed in English vs Maths in his class.
Z score for a value is defined as =(X-Mean)/Std.Dev
i.e how far is the the value from mean in terms of Std Dev.
http://web.cortland.edu/andersmd/STATS/stdscore.html
A z Scoreis an actual or raw score converted intostandard deviation (SD) units -- hence the term standard score -- sothat it can be placed on the normal distribution curve. A z score indicates how much ascore deviates from the mean of the distribution. Simply knowing a z scoreoffers no information about the raw score, but it indicates how well a persondid compared to other test-takers in the norm group.
The units of a z score are from -3 SD to +3 SD, and 0 equals the mean.Therefore, positive z scores exceed the mean, while negative z scores are lessthan the mean.
There are few good examples illustrated at site
https://statistics.laerd.com/statistical-guides/standard-score-2.php
1. How well did Sarah perform in her English Literature coursework compared to the other 50 students?
Say Sarah scored,70. Mean is 60 and StdDev is 15. Then z=70-60/15=0.667=0.67
Now but now we need to work out the percentage (or number) of students that scored higher and lower than Sarah. To do this, we need to refer to the standard normal distribution table. (https://home.ubalt.edu/ntsbarsh/Business-stat/StatistialTables.pdf)
From table, we check row 0.6 and column 0.07..value is 0.7486. i.e 74.86%
So Sarah did better than 74.86% students of the class.
2.How well did Sarah perform in her Maths coursework compared to her English Literature coursework?
Clearly, the two scores (her English Literature and Maths coursework marks) come from different distributions. The distribution of 50 students that completed the English Literature coursework has a mean of 60 and standard deviation of 15. The distribution of 50 students that completed the Maths coursework, on the other hand, has a mean of 68 and a standard deviation of 6. This gives us the following:
| Score | Mean | Standard Deviation | |
| (X) | µ | s | |
| English Literature | 70 | 60 | 15 |
| Maths | 72 | 68 | 6 |
Since these scores are from two different distributions, we need to standardise them into z-scores so that they can be directly compared. This gives us:
The z-scores highlight that the student is two thirds (z = 0.67) of a standard deviation above the mean in English Literature, but also two thirds (z = 0.67) of a standard deviation above the mean in Maths. Using the standard normal distribution table, we can see that Sarah clearly performed above 'average' in both subjects although again, around 25% of the class got a better mark than her. However, the key point her is that the standard score showed that Sarah performed equally well in her English Literature and Maths coursework, even though her marks were different in both pieces. This shows the usefulness of the standard score statistic.
(Please refer https://statistics.laerd.com/statistical-guides/standard-score-4.php)
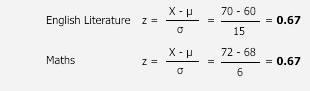

Comments
Post a Comment